
1. 고성능 곱셈기의 구현 방법
곱셈은 일반적으로 덧셈보다 복잡하고 시간이 오래 걸리는 연산이다. 여러 가지 방식을 통해 연산 속도를 향상시킬 수 있다. 그 중 생각해본 방법은 Booth Encoding을 이용해 Partial Product를 줄이는 방법과 TDM 방식이다.
TDM은 “A method for speed optimized partial product reduction and generation of fast parallel multipliers using an algorithmic approach”에 따르면 vertical compressor slice를 이용하여 3차원으로 Partial Product를 줄이는 방법이다.
V. G. Oklobdzija, D. Villeger와/과S. S. Liu, “A method for speed optimized partial product reduction and generation of fast parallel multipliers using an algorithmic approach”, IEEE Transactions on Computers, vol 45, 호 3. Institute of Electrical and Electronics Engineers (IEEE), pp 294–306, 3-1996.


TDM 곱셈기를 실제 구현한 결과 Booth Encoding을 이용한 방법보다 성능이 나오지 않는 것을 확인할 수 있었는데, 이는 SUM을 만드는 시간보다 CARRY를 만드는 시간이 더 빠르다는 TDM에서 주요 아이디어가 간과하였기 때문이다. Multi-input gate를 이용하면 SUM을 만드는 시간보다 CARRY를 만드는 시간이 더 빠르다는 이점을 충분히 이용할 수 없게 된다. 아래는 TDM을 이용한 곱셈기를 설계한 결과이다.



이 방법은 radix-2를 사용해 전혀 Partial Product를 줄이지 않은 Original TDM 곱셈기이다. 비록 Booth Encoding을 사용한 방법보다 빠르지는 않지만 뒤에서 나올 Booth Encoding과 함께 사용하여 곰셈기의 성능을 더 높일 수 있었다.
Booth Encoding을 이용한 방법은 radix-4, radix-8, radix-16을 사용한 방법을 모두 생각해 보았다. 그 중 radix-4, radix-8을 실제로 구현해보았고 radix-16은 구상 단계에서 radix-4보다 느리다는 것을 확인할 수 있었다. 9x7의 곱셈은 연산을 수행하는 숫자의 bit가 적기 때문에 radix-4가 가장 효율적이다.
1) radix-4
실제로 구현을 한 곱셈기이다. ‘2’번 파트에서 자세히 설명한다.


2) radix-8
Partial Product의 계산 단계가 4개로 radix-4와 다르지 않기에 더 빠르지 않다. 3Y를 처리해주기 위해 Y와 2Y를 4비트씩 더해주는 방법을 생각했다.
이 방법에 관해서는 다른 포스트를 확인해 보기를 권장합니다.
포스팅 보러가기



3) radix-16
Partial Product의 계산 단계를 2단계로 줄일 수 있지만 Booth Encoding 단계에서 많은 시간이 소요되기에 곱셈을 하는 수가 큰 경우에 유효가 있다는 것을 알 수 있었다. Base에 Weight를 더하거나 빼주는 방식으로 ± Y ~ 7Y를 모두 구현할 수 있다. Partial Product를 만드는데 #(1.9, 4.6)의 시간이 걸리는 것을 알 수 있다.

결과적으로 radix-4를 설계하였다. TDM은 최대 3.6ns, radix-4는 최대 3.4ns, radix-8은 최대 4ns가 나왔다. radic-16은 더 많은 시간이 걸릴 것으로 예상이 된다.
2. 설계한 곱셈기 설명
위에서 설명했듯이 결과적으로 radix-4를 설계하였다.

1) Booth Encoder


Booth Encoder는 각 3개씩 묶은 결과가 Y, 2Y, -Y, -2Y 중 어떠한 값이 될지 결정해준다. S는 sign bit로 부호를 말한다. 이 결과는 아래 Booth Selector로 들어간다.
Y인지 판단하는 M을 만들기 위해 XOR Cell이 하나 쓰였다. XOR Cell은 그림 8과 같이 구현하였다.
2Y인지 판단하는 2M을 만들기 위해 3bit NAND가 3개 사용되었다.
* 2bit XOR Cell


2) Booth Selector


Booth Selector는 Booth Encoder로부터 받은 M과 2M을 가지고 Y와 2Y 중 어느 것을 선택할지 결정한다. 그 후 sign bit에 따라 1의 보수를 취해준다. 2의 보수를 취하기 위해 나중에 Sign bit를 partial product 결과의 LSB에 더해준다.
Y, 2Y를 선택하기 위해 2bit NAND가 3개가 사용되었다.
1의 보수를 취해주기 위해 XOR Cell이 하나 쓰였다.
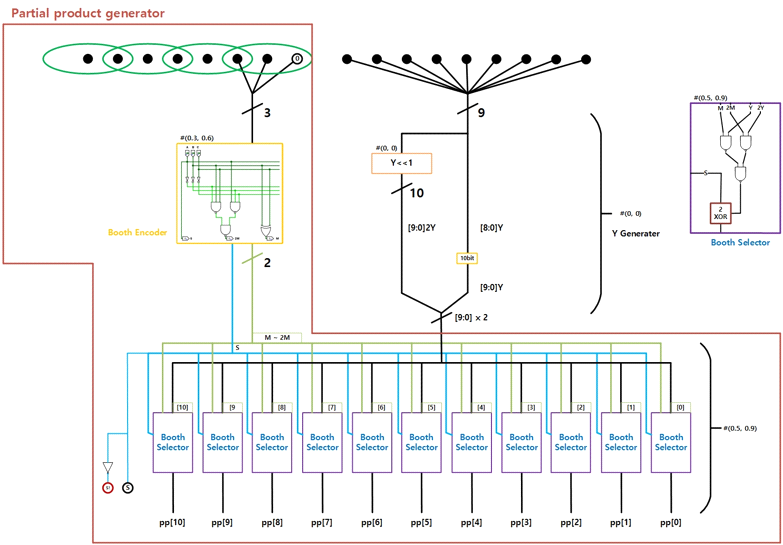
3) Partial product generator

위에서 만든 1) Booth Encoder와 2) Booth Selector를 인스턴스화하여 Partial product generator를 만들어 주었다. Booth Encoder에서 만들어진 결과가 Booth Selector 10개로 들어가 Partial product를 만들어 출력한다.
4) Y, 2Y 생성


Y와 2Y를 만들기 위해 그림 11과 같이 선언해주었다. 2Y는 왼쪽으로 1bit shifting해줘야 하는데, 이는 LSB에 0을 추가해줌으로써 구현할 수 있었다. 이렇게 하면 게이트를 추가적으로 소모하지 않고 Shifting이 가능하다.
5) Patial Product 생성

위에서 만든 3) Partial product generator를 인스턴스화하여 Patial Product 생성해 주었다.
wire [9:0] w_pp_F1 ~ w_pp_F4는 Partial product generator에 만들어진 결과이다.
wire [15:0] w_pp_F1_result ~ w_pp_F4_result는 sign bit를 포함해 자리수를 맞춰줘 16bit로 만들어준 결과이다.
6) Carry Save Adder

위 1) ~ 5)로부터 만들어진 Partial Product를 Carry Save Adding을 통해 Partial Product의 개수를 줄여주었다. 이때, TDM 기법을 이용한 4:2 Compressor를 디자인하였다.


그림 14의 4:2 Compressor는 4개의 Partial Product 입력과 Cin 하나를 받아, 다음 Compressor로 들어가는 Cout과 결과로 출력되는 Carry, Sum을 만든다. 다음 Compressor로 들어가는 Cout은 Carry, Sum보다 연산이 빨리 끝나고 이를 다음 단계 입력으로 넣어줌으로써 계산 시간을 단축시켜 줄 수 있다. 아래 그림 15는 4:2 Compressor의 critical path이다.

그림 15를 보면 이전 carry가 전파되는 것보다 XOR 2개를 지나는 시간이 더 길다는 것을 알 수 있다. 이는 TDM을 이용한 Compressor cell의 이점이다.
추가적으로 Carry Save Adding에 사용된 Compressor cell은 다음과 같다.
4:2 Compressor
Carry를 받지 않는 4:2 Compressor이다.


3:2 Compressor
Carry를 받는 3:2 Compressor와 받지 않는 3:2 Compressor이다. Carry를 받는 받지 않는 3:2 Compressor는 FA와 같다.




2:2 Compressor
Carry를 받는 2:2 Compressor인 FA와 받지 않는 2:2 Compressor인 HA이다.




추가적으로 Compressor cell에 사용된 XOR, MAJ Cell은 다음과 같다.







위 Compressor cell들을 이용해 그림 20과 같이 압축할 수 있다.

7) Carry Ripple Adder - Kogge-Stone Adder using Higher Valency Cell
2번째 설계에서 만들었던 Kogge-Stone Adder using Higher Valency Cell Adder를 사용하여 압축된 csa_in_0, csa_in_1를 덧셈을 해주면 원하는 결과를 얻을 수 있다. Kogge-Stone Adder using Higher Valency Cell Adder는 두 번째 보고서에서 자세히 설명하였기에 설명을 생략하였다.

3. 결과 Waveform / 정확도 검증
1) 정확도 검증 방법
정확도는 Test Bench를 작성하여, 곱셈기에 들어갈 수 있는 모든 수를 넣어봄으로써 검증하였다.
[ Test Bench ]


Test Bench는 2가지 모드로 쓸 수 있도록 설계하였다. 기본적으로는 곱셈기에 들어갈 수 있는 모든 수를 넣어 테스트해주는 코드를 실행한다. 가장 위에 선언된 `define문의 주석 처리를 해제하면 직접 입력한 값에 의한 시뮬레이션을 할 수 있다. 이 값은 설계 조건으로 주어진 값들이다. 아래는 `define문을 주석 처리하여 입력한 값에 대한 결과이다.
(1) 임의의 시점에서 Waveform 결과

Waveform을 보면 설계한 곱셈기가 문제없이 동작함을 알 수 있다.
(2) 콘솔 결과



그림 24는 콘솔 출력 결과로 일부분을 잘라 보여준다. 모두 정상적으로 출력하는 것을 알 수 있고 error가 0으로 정답과 설계한 곱셈기의 결과가 전부 일치함을 알 수 있다.
2) 설계한 곱셈기의 지연 분석
그림 22 Test Bench의 `define문을 주석 처리를 해제하고 실행하면, 주어진 값들에 대해서 시뮬레이션을 수행할 수 있다.

그림 25의 실행 결과를 보면 값들이 정상적으로 계산되어 나온 것을 확인할 수 있다.

설계한 곱셈기의 가장 긴 Delay는 in1 = 7’h00, in2 = 9’h00을 계산한 후 in1 = 7’h00, in2 = 9’h00을 계산할 때이며 이는 3.5ns이다.
추가적으로 아래 그림 27은 설계한 곱셈기의 모든 지연이다.


3) 설계한 곱셈기의 critical path 분석

위 그림 29는 설계한 곱셈기의 critical path이다. Booth Encoder에서 2개의 2bit XOR를 사용한 뒤, Booth Selector에서 2개의 2bit NAND를 사용한다. 이렇게 생성된 partial product는 4:2 Compressor를 통해 2개의 3bit XOR를 거치게 된다. 그 후, 마지막 CPA에서 1개의 2bit XOR, 4개의 4bit Higher Valency Cell, 1개의 2bit XOR를 순서대로 소모하게 된다.
즉, 최대 4개의 2bit XOR + 2개의 3bit XOR + 2개의 2bit NAND + 4개의 4bit Higher Valency Cell을 거친다.
4bit Higher Valency Cell은 2개의 4bit NAND만큼의 delay를 가진다.

4. 결론
Booth Encoding을 radix-4를 이용하여 구현하였고 나온 partial product는 TDM 4:2 Compressor를 이용하여 압축하였다. 그리고 최종적으로는 Kogge-Stone Adder using Higher Valency Cell CPA를 사용하여 결과를 얻었다.
이 과정에서 Booth Encoder, Booth Selector, CSA, CPA 등을 디자인하였다.
설계한 곱셈기의 가장 긴 Delay는 3.5ns이다.
가장 긴 Delay가 나올 수 있는 critical path는 4개의 2bit XOR + 2개의 3bit XOR + 2개의 2bit NAND + 4개의 4bit Higher Valency Cell을 거치는 경우이다.
정확도는 Test Bench를 작성하여, 곱셈기에 들어갈 수 있는 모든 수를 넣어봄으로써 검증하였다. 그 결과 모든 값의 결과가 올바르게 나온 것을 확인할 수 있었다.
이번 설계를 진행하면서 고성능 곱셈기를 만들 수 있는 다양한 방법에 대해서 알 수 있었고, 직접 만들어 보면서 그 원리를 더 자세히 알 수 있었다. 아쉬운 점은 radix-8, radix-16을 사용하는 곱셈기를 설계하려 했지만, 곱셈의 bit가 적어 성능이 오히려 나빠져 사용하지 못했다는 점이다.
C
Contents



