
1. Kogge-Stone Adder
연산 속도가 빠른 Adder는 Group PG에서의 Logic level의 수가 가장 적은 Adder를 구현함으로써 만족할 수 있다. Tree Adder 중에 Logic level의 수가 가장 적은 Adder는 Kogge stone Adder이고, Kogge stone Adder는 아래와 같이 4개의 Logic level을 갖는다.
출처: CMOS VLSI Design A Circuits and Systems Perspective, 4th Edition
이러한 Kogge stone Adder는 wiring track이 8개이고, 만약 Carry_in을 고려하면 9개의 wiring track이 발생한다. 이 wiring track이라는 단점과 trade off하여 적은 Logic level로 빠른 성능을 보여준다.
아래는 Carry_in을 고려한 Kogge stone Adder이다.
위 그림 2의 Kogge stone는 higer valency cell을 이용해 logic level을 줄일 수 있다.
2. Kogge-Stone Adder using Higher Valency Cell
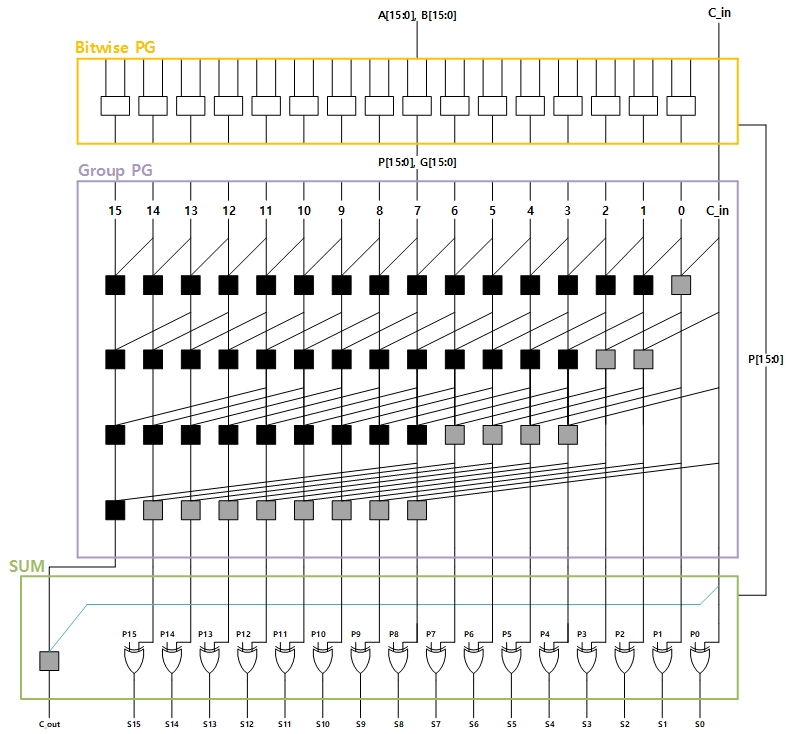
아래 그림 4는 higer valency cell을 이용해 설계한 Kogge stone Adder이다.
Bitwise PG Logic에서 입력에 대해서 각각 Bitwise연산을 수행해 Propagate와 Generate한다. 이 Propagate와 Generate된 결과는 Group PG Logic으로 들어가서 higer valency cell을 거쳐서 각각 n : C_in까지 Generate한 결과를 출력한다.
이때, 2 Stage의 Black higer valency cell은 최대 4개의 input을 받으므로 15:0까지의 결과만 출력할 수 있다. 이는 나중에 SUM Logic에서, G(15:0)와 C_in을 Gray cell로 연산함으로써 C_out을 처리해주었다.
마지막으로 SUM Logic에서는 Bitwise PG Logic에서 나온 Propagate된 결과와 Group PG Logic의 Group Generate한 결과를 XOR 연산을 해줘 결과값을 구할 수 있다.
이렇게 설계한 결과 일반 Kogge stone Adder의 4 Logic level을 2Logic level로 줄일 수 있었다.
3. Verilog Code Review
Basic Gate/Cell Define
1) XOR GATE

SUM Logic에서 사용할 XOR를 만들어 주었다. nand와 nor만 사용해야 되기에 위와 같이 nand로 디자인해주었다.
2) Generate & Propagate Cell

Bitwise Logic에서 각 비트를 Generate, Propagate 해줄 Generate & Propagate Cell를 정의해주었다. Generate는 AND 연산으로 만들어지고, Propagate는 XOR 연산해서 만들어진다. 이를 위와 같이 구현하였다.
3) Gray Cell

2bit Gray cell을 정의해주었다. And-Or 연산을 수행한다. nand로 바꾸어 구현해주었다. 다음과 같은 로직 연산을 수행한다.
Ga:b = Pa Gb + Ga
4) 3-higher valency Gray Cell

a의 P, G, b의 P, G, c의 G를 받아 Generate하는 3 input higher valency Gray Cell을 만들었다. 다음과 같은 로직 연산을 수행한다.
Ga:c = Pa Pb Gc + Pa Gb + Ga
5) 3-higher valency Black Cell

a의 P, G, b의 P, G, c의 P, G를 받아 Generate, Propagate하는 3 input higher valency Black Cell을 만들었다. 다음과 같은 로직 연산을 수행한다.
Ga:c = Pa Pb Gc + Pa Gb + Ga
Pa:c = Pa Pb Pc
이번 설계에서 사용하지는 않았지만 통일성을 위해 만들어주었다.
6) 4-higher valency Gray Cell

a의 P, G, b의 P, G, c의 P, G, d의 G를 받아 Generate하는 4 input higher valency Gray Cell을 만들었다. 다음과 같은 로직 연산을 수행한다.
Ga:d = Pa Pb Pc Gd + Pa Pb Gc + Pa Gb + Ga
7) 4-higher valency Black Cell

a의 P, G, b의 P, G, c의 P, G, d의 P, G,를 받아 Generate, Propagate하는 4 input higher valency Black Cell을 만들었다. 다음과 같은 로직 연산을 수행한다.
Ga:d = Pa Pb Pc Gd + Pa Pb Gc + Pa Gb + Ga
Pa:d = Pa Pb Pc Pd
Bitwise PG Logic

입력으로 들어온 각 비트들에 대해 Generate와 Propagate를 만들어주는 Bitwise PG Logic이다. 0~15까지 각각 연산을 해주는 Logic을 generate문을 통해 구현해주었다.
Group PG Logic

Bitwise PG Logic에서 만들어 준 P와 G를 Group PG 연산해주는 Logic이다.
- Gray Cell 1개
- 3-Higher valency Gray Cell 1개
- 4-Higher valency Gray Cell 1개
- 4-Higher valency Black Cell 13개
- Gray Cell 4개
- 3-Higher valency Gray Cell 4개
- 4-Higher valency Gray Cell 4개
- 4-Higher valency Black Cell 1개
여기서 Cin을 받지 못한 G15:0는 SUM Logic에서 Gray Cell을 이용해서 처리해준다.
SUM Logic

Bitwise PG Logic에서 만들어진 P와 Group PG Logic에서 만들어 준 GG를 최종 SUM 연산을 수행해주는 Logic이다. XOR연산을 수행하며, Gray Cell로 전 Group PG Logic나온 G15:0, P15:0을 C_in과 Gray cell 연산을 통해 G15:C_in으로 만들어 최종 C_out으로 만들어준다.
XOR의 critical path는 nand 3개를 지나는데, Gray cell의 critical path는 nand 2개이다. 그렇기 때문에 SUM Logic의 critical path는 C_out을 지나지 않게 된다.
4. 결과 Waveform / 정확도 검증
Test Bench

Test Bench는 2가지 모드로 쓸 수 있도록 설계하였다. 기본적으로는 10000번의 random값을 넣어 테스트해주는 코드를 실행한다. 가장 위에 선언된 `define문을 주석 처리하면 직접 입력한 값에 의한 시뮬레이션을 할 수 있다. 아래는 `define문을 주석 처리하여 입력한 값에 대한 결과이다.
1) 결과 Waveform
2) 정확도 검증
설계한 모듈의 정확도를 검증하기 위해 입력에 값을 넣어 그 값이 맞는 지 확인하는 작업을 진행한다. 이때, 16bit x 16bit로 구현할 수 있는 연산을 모두 검증해보면 좋겠지만, 그렇게 된다면 0을 포함하여 65536 x 65536 = 4,294,967,296개의 연산을 수행해야 한다. 또한, Vivado에서 이를 일일이 다 비교해야 하기에 시간이 오래 걸린다. 그렇기 때문에 10000번의 random 숫자를 생성하여 검증하는 것으로 하였다.
위 Test Bench코드에서 `define문을 선언하고 실행한 결과이다. 랜덤값을 (+)연산한 결과와 비교하여 값이 다르면 error를 표시해주는 코드이다.
- $urandom%65536 // 0~65535의 랜덤값을 만들어준다. 16비트는 0~65535의 값을 만들 수 있다.
- ((o_c«16) + o_s) // 캐리는 65536과 같으므로 shift해주고 o_s와 더해주면 최종값을 만들 수 있다.


검증 결과 문제없이 ADDER가 동작하고 있음을 확인할 수 있었다. error는 0으로 정상적으로 작동한다.
5. 성능 최적화 방법 / 성능 분석
1) 성능 최적화 방법
- Higher Valency Cell 사용하여 Logic level 감소, 게이트 여러 개 쓰는 것보다 delay 감소
- Generate & Propagate Cell에서 AND gate를 직접 사용하지 않고 XOR gate 중간에서 사용하여 게이트 절감
- Group PG Logic에서 15:C_in을 구하는 것이 아닌 15:0을 구하여 SUM Logic에서 연산함으로써 Logic level 감소
2) 성능 분석
Adder의 Delay는 각 Gate가 가지고 있는 지연 성분에 의해 발생한다. 위는 설계한 Adder의 Critical Path를 나타낸 것이다. 실제 확인해 보기 위해 시뮬레이션을 해보면 아래와 같이 결과를 얻을 수 있다.
Kogge-Stone Adder using Higher Valency Cell
Original Kogge stone
16’h0 + 16’h0 (C_in: 0)일 때의 결과를 살펴보면 Original Kogge stone은 1700ns의 delay가 발생한다. Kogge-Stone Adder using Higher Valency Cell은 1400ns의 delay로 delay가 감소한 것을 확인할 수 있었다.
Kogge-Stone Adder using Higher Valency Cell
Original Kogge stone
16’hffff + 16’h1 (C_in: 0)일 때의 결과를 살펴보면 Original Kogge stone은 2000ns의 delay가 발생한다. Kogge-Stone Adder using Higher Valency Cell은 1800ns의 delay로 delay가 감소한 것을 확인할 수 있었다.
6. 다른 설계 방식
실제 설계를 진행하지는 않았지만 고안한 방법이다. sparse-tree Adder로 SUM Logic의 빨간 블록은 Carry Lookahead Adder이다. Group PG Logic에서 계산되는 동시에 빨간 블록도 동시에 계산을 한다. 이렇게 나온 값은 이전 Carry에 의해 선택되는 구조이다.
이렇게 설계를 하면 Higher Valency Cell만을 사용한 Kogge stone보다 적은 로직을 사용할 수 있다는 장점이 있다. 성능을 비교해보면, 빨간 블록의 계산 부분은 Group PG Logic과 같이 계산되기에 제외하고 XOR로 선택되는 부분만 남는다. 이렇게 되면 기존의 Higher Valency Cell만을 사용한 Kogge stone와 비슷한 성능을 가질 수 있다.
Higher Valency Cell만을 사용한 Kogge stone보다 적은 로직을 사용할 수 있다는 장점이 있음에도 이번 프로젝트의 목적인 성능을 개선할 수는 없기에 실제로 설계는 하지 않고 스케치만 진행하였다.
C
Contents



