
1. 설계 주제
DC 모터의 위치 제어기 설계

위 그림 1은 설계에 사용할 서보모터의 전달함수 모델이다. 여기서 am은 600, bm은 30이다. Ω0는 모터의 속도이며 이 모터의 속도에 적분기가 붙어 최종적으로 모터의 위치 θ0가 출력되는 시스템이다. 이 시스템에 제어기를 붙여 제어한다.
2. 설계 제한 요소
1) 경제적 제한 조건: 모터에 인가되는 증폭기의 용량을 가능한 적게 하여 비용을 낮게 한다. (K값을 가능한 적게)
2) 생산성과 내구성: 가능한 빠른 시간 내에 목표치(스텝 입력)에 도달하도록 해야 한다. 또한, 모터를 가능한 오래 사용할 수 있는 제어기를 설계해야 한다. (ocillation은 가능한 적게, 즉, settling time이 적게)
3) 폐루프의 dominant pole의 damping ratio는 0.4~0.7사이의 값이어야 하며, settling time은 1/30sec보다 작아야 한다.
4) 가능한 phase margin(최소한 40도 이상)이 커야 한다.
5) 경제적 제한 요소와 생산성과 내구성이 서로 갈등 관계이면 각각의 비용을 가정(가정한 이유를 설명)하고 이에 비용을 최소화할 수 있도록 한다.
3. 설계 과정
1) 제어기 결정
현재 주어진 plant의 전달함수는 다음과 같이 쓸 수 있다.
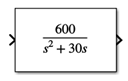
분모의 차수는 2차인데, 만약 PI 적분기나, PID 적분기를 추가하게 된다는 분모의 차수는 3차를 넘어간다. 이렇게 설계를 하면 3차 이상인 시스템을 2차로 근사를 하여 파라미터를 구해야 한다. 그렇기에 설계의 편의성을 위해 PD 제어로 제어하는 것을 선택하게 됐다. 또한, PD 제어기를 사용하여 제어함으로써 시스템의 안정도를 개선하고 좋은 동적 응답(과도 응답 속도가 증가하고, 오버슈트가 줄어듦)의 효과를 얻을 수 있다.
아래는 PD 제어기를 포함한 시스템 모델을 나타내었다.
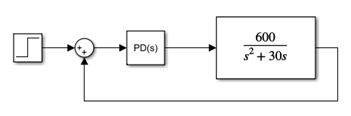
2) 파라미터 설정
damping factor
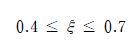
ωn
ωn은 주어진 settling time으로부터 구할 수 있다.
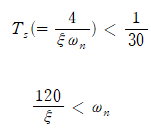
정리하면 ωn은 ξ에 대한 식으로 정리를 할 수 있다. 즉,ξ를 정하면 ωn도 정해진다.
P.O.
P.O.는 ξ에 대해 나타낼 수 있으며, ξ를 대입했을 때 다음과 같은 범위로 주어진다.
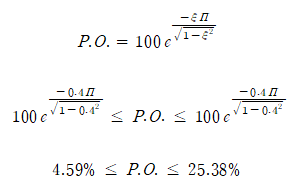
Kp, Kd
Kp와 Kd는 2차 시스템의 식을 정리함으로써 구할 수 있다. 위 그림3의 시스템을 정리해보면 다음과 같다.
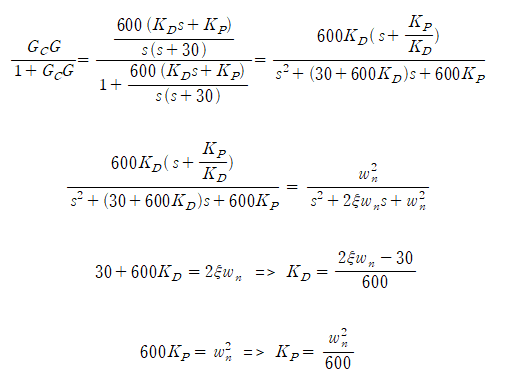
Kd는 ξ, ωn에 대해서 나타낼 수 있으며, Kp는 ωn에 대해서 나타낼 수 있다.
위 파라미터들은 ξ를 결정함으로써 전부 결정할 수 있다는 것을 알 수 있었다. 아래 그림 4는 ξ를 변화시켰을 때, 각 파라미터의 범위를 엑셀을 이용하여 구한 것이다.
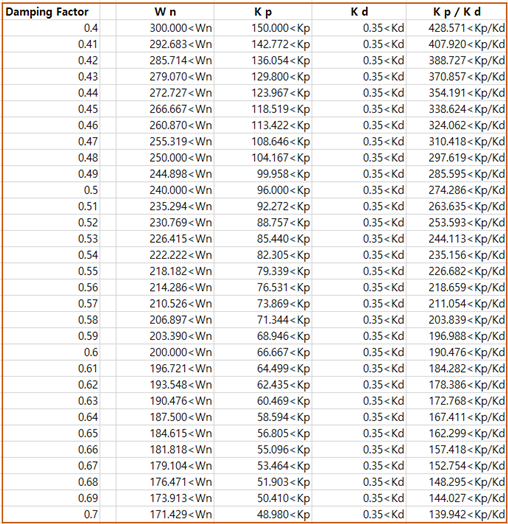
여기서 Kp/Kd는 Kp 범위를 Kd 범위로 나눠줌으로써 구할 수 있다.
3) Root Locus을 이용한 이득 구하기
Root locus는 어떤 시스템의 파라미터가 변화할 때 이에 따라 반응하는 시스템의 pole 위치 변화를 그래프 형태로 묘사한 것을 말한다. 여기서 파라미터는 K 이득을 말한다. 2차 시스템에서 이득은 Kd와 Kp 2개가 존재하기에 하나의 값은 고정을 해야 한다.
ξ를 임의로 설정하고, Kp/Kd를 임의로 설정하여 Root locus에서 만족하는 점을 찾으면 시스템의 Kd 이득을 찾을 수 있다. Root locus로 Kp를 찾는 것이 아닌 Kd를 찾는 이유는 그림 5의 정리된 식을 보면 알 수 있다.
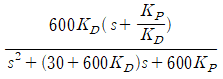
Root locus를 이용할 때, 구하려는 이득을 앞으로 빼는데, 위 그림 5를 보면 Kd를 분수 밖으로 뺄 수 있기에 Kd의 이득을 먼저 찾기로 한다. 물론 Kp/Kd와 Kd가 결정되면 Kp도 자동으로 얻을 수 있다.
우선 Damping Factor가 0.55일 때, Kp/Kd를 그림 4의 범위 226.682보다 큰 230으로 설정하여 시뮬레이션을 하였다. 그 결과는 그림 6과 같다.
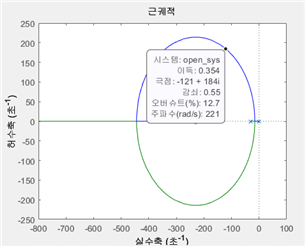
Root locus 그림에서 설정한 damping factor = 0.55의 값의 점을 찾으면 이득을 알 수 있다. 이때의 이득은 0.354이고 이는 Kd의 이득이다. 이때, P.O.가 다음을 만족함을 알 수 있다.
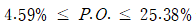
4) 조건에 맞는지 확인하기
위 3)에서 구한 Kd를 넣고 bode plot과 step 입력에 대한 출력을 구한다.
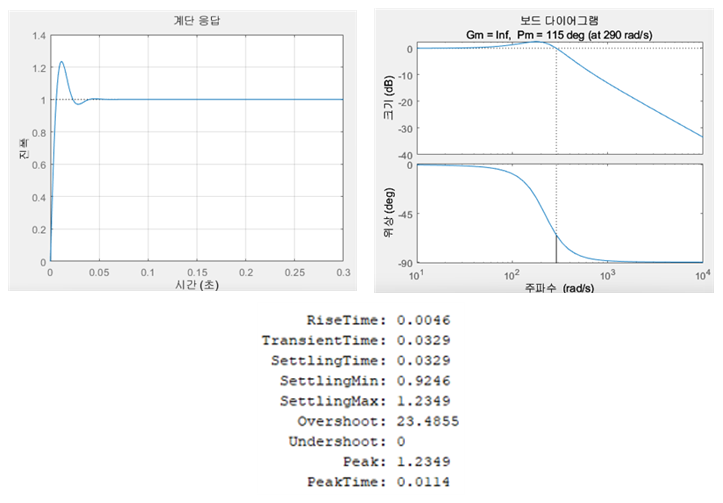
그림 7을 보면 초기에 설정한 settling time 0.033333에 간신히 들어온 것을 알 수 있었고 phase margin이 40도 이상으로 만족함을 알 수 있다
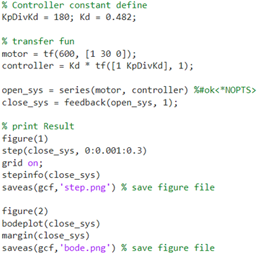
Root locus와 bode plot, step 입력에 대한 출력을 내보내는 matlab의 코드는 다음 그림 8과 같다.
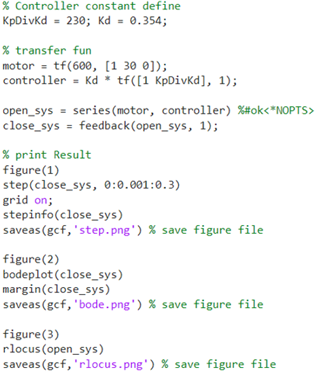
변수 KpDivKd는 Kp/Kd를 의미하며 damping factor와 같이 초기에 설정해주는 값이다.
Kd는 이득으로, Root locus를 출력할 때는 1로 둔다. Root locus에서 이득을 구하면 그 값을 넣어주어 step과 bode plot을 얻을 수 있다.
motor는 plant의 전달함수로 적분기를 포함한 전달함수이며, controller는 PD제어기를 나타내는 전달함수이다.
motor와 controller를 직렬로 연결한 전달함수는 open_sys이며, 이는 Root locus를 구할 때 사용하는 전달함수이다.
open_sys를 feedback 함수로 연결함으로써 close_sys, Closed loop 전달함수를 얻을 수 있었다.
figure(1), figure(2), figure(3)는 각각의 그림을 따로 뽑기 위해 설정하였다.
그 후, step()을 이용해 step 입력을 줬을 때의 출력, bodeplot()을 이용해 bode plot, rlocus()를 이용해 Root locus의 그림을 얻을 수 있었다.
stepinfo()는 RiseTime, SettlingTime과 같은 파라미터를 보기 위해 사용하였다.
그 외에 grid 설정, 그림 저장을 위한 saveas() 함수를 사용하였다.
5) 최적의 조건 구하기
위 4)번에서 만족하는 결과를 찾을 수 있었지만, 최적의 설계를 위해 여러 값들을 넣어 시뮬레이션하였다. 아래 그림 9는 시뮬레이션 결과를 정리한 표이다. 이 표가 나오는 과정은 3)~4) 과정을 반복하였다. 자세한 그림과 코드, 과정은 6. 첨부에 포함하였다.

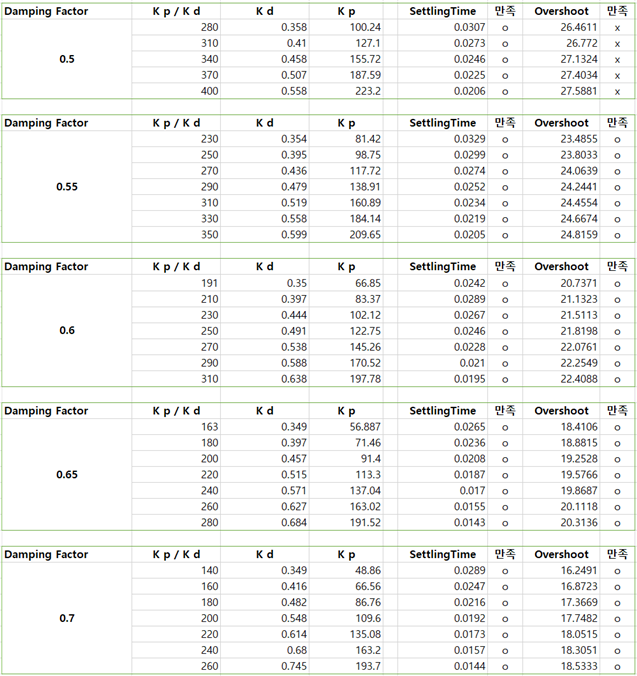
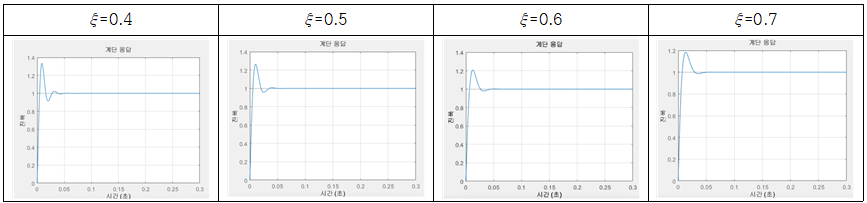
우선 damping factor는 0.7로 선정하였다. 선정한 이유는 아래 그림 10과 같다. ξ가 커질수록 시스템의 overshoot가 작아지기에 가장 overshoot가 적고 ocillation이 적은 0.7을 택하였다.
damping factor가 0.7일 때, K와 settling Time은 서로 갈등 관계에 있다. 즉, 경제적 제한 요소와 생산성과 내구성이 서로 갈등 관계에 놓여 있다고 할 수 있다. 그렇기 때문에 서로의 타협점을 찾아야만 했다.
K에 따른 비용 산출
K는 이득이다. 즉, 앰프를 이용하여 만들어 내야 한다. 많이 쓰이는 op-amp 중에서 LM741칩을 사용한다고 가정한다.

이 칩은 최소 50의 gain, 최대 200의 gain을 얻을 수 있다. Kd에 하나, Kp에 하나 사용한다고 생각하면 된다. 이 칩의 가격은 아마존에서 20개에 $12.52(\16,927)이다. 즉, 하나당 846원이며 2개가 필요하니 1,692원이 필요하다. 비용을 최소화하면서 큰 이득을 얻으려면 Kp, Kd는 200보다 작은 이득을 이용해야 한다. 만약 200을 넘어가게 된다면 추가적인 gain을 얻기 위해 칩이 하나 더 사용되어야 한다.
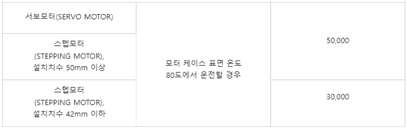
생산성과 내구성에 따른 비용 산출
서보 모터는 표면 온도 80도에서 운전을 할 경우 최대 50,000시간이 사용이 가능하다.
서보 모터는 디바이스마트의 아래와 같은 모터를 이용한다고 했을 때 6,500원이 든다.

비용 산출
위의 결과를 토대로 비용을 산출해보면 다음과 같다.
최대 운전 시간은 20,000시간으로 가정하였다.
op-amp의 비용: 1,692원
모터의 비용: 6,500원
여기서 K를 더 키워 op-amp를 더 사용한다면 op-amp의 비용이 증가하므로, 최적의 값은 op-amp를 Kp, kd에 하나씩 이용하는 것이다. 또한, 이득은 각각 200보다 작아야 한다. 이를 바탕으로 산출하면 다음과 같은 값을 선정할 수 있었다.
6) 최종 설계 결과
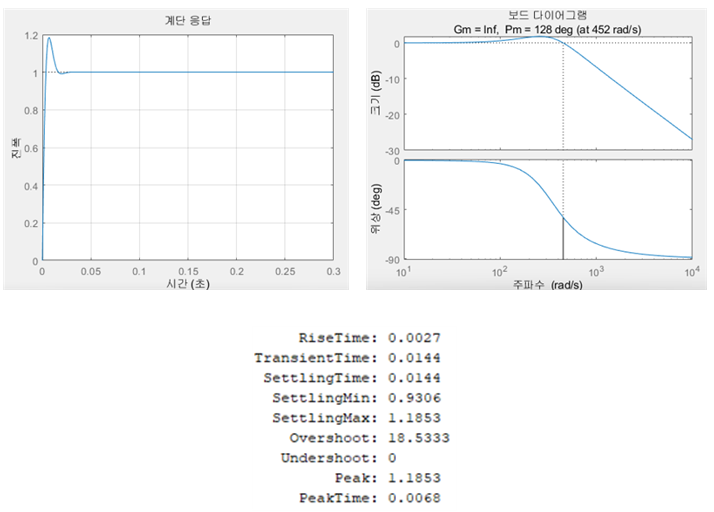
최종 설계를 한 결과에 대한 파라미터는 아래 그림 15와 같다.

그에 따른 bode plot, step 입력에 대한 출력의 결과는 다음 그림 16과 같다.
settling Time은 0.0144으로 0.03보다 작으므로 조건을 충족한다. 또한, damping Factor도 0.7로 조건을 만족하며, phase margin은 128도로 40도보다 크다. K는 비용과 생산성과 내구성을 고려하여 적절한 값을 만족했다.
4. 고찰
DC모터의 위치 제어기를 PD Controller를 이용하여 설계하였다. 각 파라미터를 설정하여 값을 지정하였고 그 과정에서 Root locus, Bode Plot, Step입력을 이용하였다. 그 결과 주어진 설계 제한 요소의 settling Time, damping Factor, phase margin을 모두 충족하는 결과를 얻을 수 있었다. 경제적 제한 요소와 생산성과 내구성 간에 갈등 관계가 발생하였으며 비용을 고려하여 설계를 하였다.
만약, K(비용) 대비 settling Time(생산성과 내구성)의 관계에 대해서만 고려해 값을 산출했더라면 아래와 같았을 것이다.
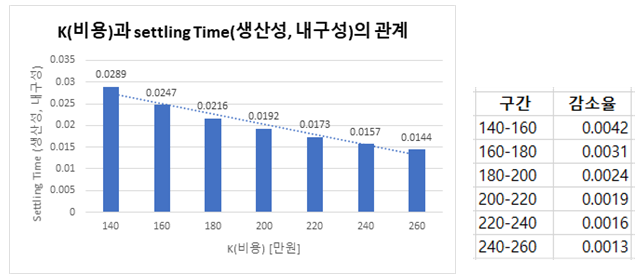
그림 17의 구간별 감소율을 보면 점점 감소율이 적어지는 것을 보인다. 이는 K가 커질수록, 즉 비용이 증가할수록 그 비용대비 얻는 성능이 적다는 것이다. 그렇기에 비용대비 큰 감소율을 보이는 구간 140-160과 160-180에는 비용을 투자할 가치가 있다는 생각을 하였다. 그래서 Kp/Kd는 180을 택하였다.
최종 설계를 한 결과에 대한 파라미터는 아래 그림 18과 같다.

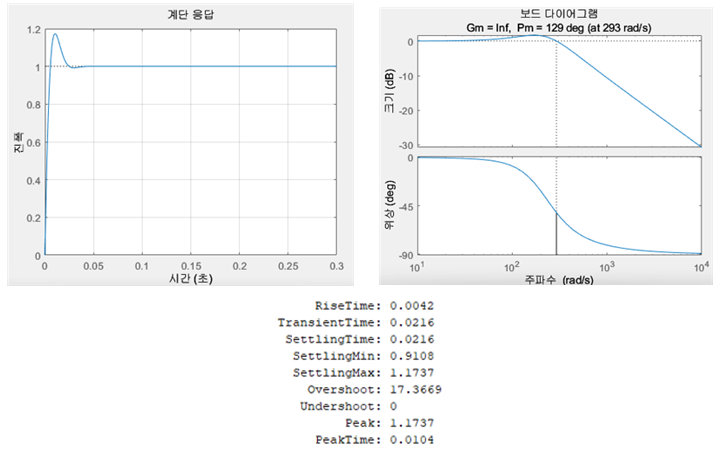
그에 따른 bode plot, step 입력에 대한 출력의 결과는 다음 그림 19와 같다.
settling Time은 0.0216으로 0.03보다 작으므로 조건을 충족한다. 또한, damping Factor도 0.7로 조건을 만족하며, phase margin은 129도로 40도보다 크다. K는 비용과 생산성과 내구성을 고려하여 적절한 값을 만족했다.
5. 참고자료
LM741 데이터 시트
https://www.ti.com/lit/ds/symlink/lm741.pdf
모터의 수명을 좌우하는 것은?
https://inaom.tistory.com/552
Texas Instrumen UA741CP OP Amp
https://www.amazon.com/Texas-Instrumen-UA741CP-General-Purpose/dp/B01KO48D5K/ref=sr_1_3?keywords=ic+741&qid=1668714216&sr=8-3
서보모터
https://www.devicemart.co.kr/goods/search?keyword_log_flag=Y&search_text=%EC%84%9C%EB%B3%B4%EB%AA%A8%ED%84%B0&q=%EC%84%9C%EB%B3%B4%EB%AA%A8%ED%84%B0&x=18&y=19
PID PID Controller, Proportional Integral Derivative Controller PID 제어기
http://www.ktword.co.kr/test/view/view.php?m_temp1=4670
C
Contents



